Test Case 4
Headland with Tidal Flow
|
|
This test case checks the ability of a model to represent 1) simplified alongshore transport, 2) implementation of open boundary conditions, and 3) resuspension, transport, and deposition of suspended-sediment. This case is based on Signell and Geyer (1991) Journal of Geophysical Research 96(C2): 2561-2575.
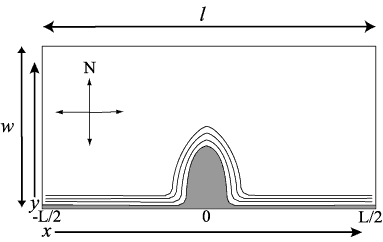
DomainThe model domain is open at the east and west ends, has a straight wall at the north end, and a parabolic headland along the south wall. Bottom SedimentSingle grain size on bottom ForcingCoriolis f = 1.0 e-4 Initial Conditionsu = 0 m³ /s Boundary ConditionsNorth, south = walls with no fluxes, no friction Output (ASCII files suitable for plotting)After 10 days : Physical ConstantsGravitational acceleration g = 9.81 m/s² NoteIf a model incorporates physical constants that differ from these, and/or automatically calculates some values specified here, please specify the values used. ResultsSolution to Test Case 4: Tidal Headland |
These pages are for communication among a group of researchers studying experimental methods of modeling and visualizing natural systems using digital (numerical) techniques. The methods and models discussed are in preliminary, developmental, stages and may be incorrect. The pages will be changed or removed without warning. The U.S. Geological Survey makes no representation as to the accuracy, correctness, or utility of any data, model, model results, or technique associated with these pages.