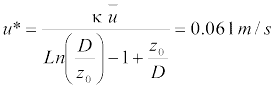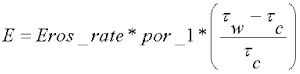|
Model:
ROMS beta v1.7.2, with sediment beta v 1.0
Date:
September 10, 2002
Modeller:
John C. Warner (jcwarner@usgs.gov), USGS Woods Hole Field Center
Channel initial conditions:
The test channel was modeled by establishing a grid parameterized with dx = 100 m , dy=100 m, f0 = 0, and h = 10 m (flat bottom). Initial conditions set a vertical logarithmic velocity profile for u (not required but provided reasonable starting values), v = 0, zeta (water surface height) = 0, SSC in the water column = 0, and bed thickness = 1 m (to provide unlimited supply). The model was forced with 2 methods :
—Simulation 1: Imposing a constant flow of 10 m³/s/m of width. This simulation allowed that water surface elevation to vary. Radiation boundary conditions were imposed for the water level along with a constant flow imposed by a depth averaged velocity ubar = 1.0 m/s at the upstream and downstream boundaries.
—Simulation 2: Imposing a constant bed slope and water surface slope of 4x10-5 m/m. This simulation forced the water surface elevation and hence the bottom stress. Radiation boundary conditions were imposed for the depth-averaged velocity along with a clamped water surface condition at each boundary. The bed slope of 4x10-5 was selected to produce a depth-averaged velocity of 1m/s (similar to simulation 1) with a Z0 = 0.005.
For both simulations, vertical mixing was parameterized using six different closure schemes: MY25, KKLpara, KKLmin, KE, KW88, and ANA
MY25 = Mellor Yamada Level 2.5 Closure, parabolic wall proximity function
KKLpara = Generic Length Scale parameterized as Mellor Yamada Level 2.5 with a parabolic wall proximity function
KKLmin = Generic Length Scale parameterized as Mellor Yamada Level 2.5 with a linear wall proximity function (minimum distance to each surface)
KE = Generic Length Scale parameterized as k-epsilon closure
KW88 = Generic Length Scale parameterized as k-omega closure
ANA = analytical expression of a parabolic vertical eddy diffusivity and viscosity profile:
Kz = k u* z (1 - z/D)
where Kz = vertical eddy viscosity, m²/s
z = height above the bottom, m
D = depth of flow, m, = 10 m
and u* = friction velocity which was calculated according to the logarithmic profile.
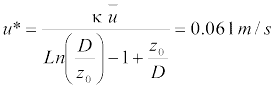
where k = 0.41 and u = 1.0 m/s.
Only suspended-sediment transport was modeled. At the center of each bottom level horizontal grid cell, the bed shear stress was estimated and used to calculate sediment resuspension using the relation:
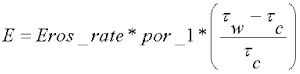
where E = erosive flux, kg/m²/s
Eros_rate = erosion rate, kg/ m²/s, set at 5.0 e - 4
por_1 = 1-porosity = 0.6
τw = shear stress exerted by the water, = ρ Cd V |V|
ρ= fluid density, kg/m³, = 998 kg/m³
V = magnitude of velocity = sqrt(u² + v²), m/s
τc = critical shear stress for erosion, = 0.05 N/m²
The erosive flux was multiplied the bed area and by dt for each grid to provide a mass of sediment (kg) that would be exchanged between the bed and the water column. Deposition was calculated from the bottom boundary condition of the settling velocity algorithm. The depositional flux was divided by the grid horizontal area to yield a mass flux in kg. The erosive flux and depositional fluxes were added at each time step to obtain a net mass transfer that was added/subtracted from the bed and added/subtracted to the bottom cell in the water column. Bed erosion was not limited because the initial depth was set at 1.0 m and the model was not run long enough to erode to this level.
Results for Simulation 1: Constant flow of 10 m3/s/m of width.
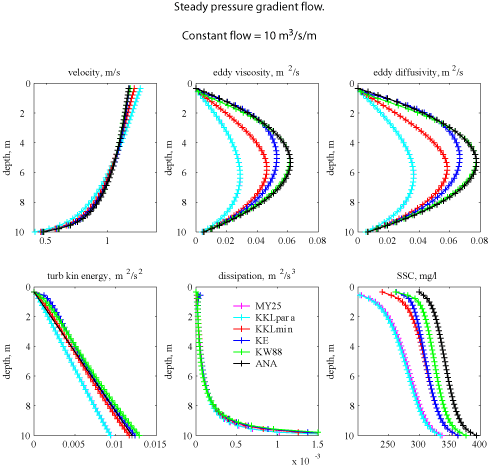
Figure 1. Vertical profiles of velocity, eddy viscosity, eddy diffusivity, turbulent kinetic energy, dissipation, and suspended-sediment concentration (SSC) for simulation 1.
For all of the vertical profiles, the solutions for MY25 are consistent with the solutions of GLS as KKLpara. This is to be expected because there are no buoyancy terms (see test case 2 - estuary case, for differences that arise due to the length scale limitations imposed by the 2 methods). Typically, the vertical profiles from the KW88 method agree most closely with the analytical solution. The turbulent kinetic energy for the MY25 (and KKLpara) method has a lower value near the bed that is compensated for by a larger water surface slope (not shown).
Results for Simulation 2: Constant bed slope and water surface slope of
4x10-5 m/m.
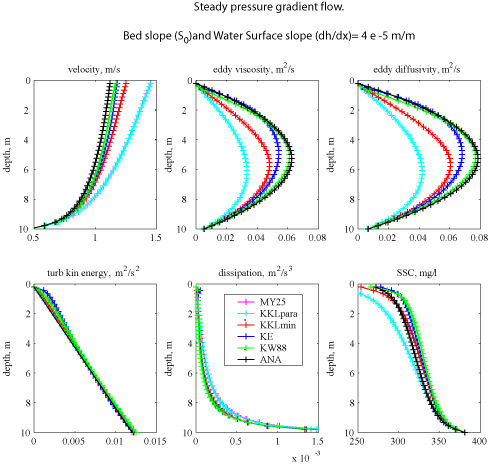
Figure 2. Vertical profiles of velocity, eddy viscosity, eddy diffusivity, turbulent kinetic energy, dissipation, and suspended-sediment concentration (SSC) for simulation 2.
For all of the vertical profiles, the solutions for MY25 are consistent with the solutions of GLS as KKLpara (as for simulation 1). Typically, the vertical profiles from the KW88 method agree most closely with the analytical solution. The turbulent kinetic energy for all simulations are now consistent because the stress is the same for each closure.
 

These pages are for communication among a group of researchers studying experimental methods of modeling and visualizing natural systems using digital (numerical) techniques. The methods and models discussed are in preliminary, developmental, stages and may be incorrect. The pages will be changed or removed without warning. The U.S. Geological Survey makes no representation as to the accuracy, correctness, or utility of any data, model, model results, or technique associated with these pages.
|